
(Note: at the top of the page you can choose translation of this article to other languages, but don't expect the translation to be perfect — "Välj språk" means "Choose language")
Föreliggande artikel utgör del 2 av 2 artiklar om lyftkraft. Klicka här för att komma till del 1 (Varför flyger flygplan?).Inom vetenskapen kan man ibland, när det gäller komplicerade teorier, förklara samma sak på flera olika sätt (med hjälp av olika modeller).
Under kvantmekanikens barndom fanns två modeller, vilka båda fortfarande används; Schrödingers (som använder integraler) och Heisenbergs (som använder matriser). Dessa två modeller ser helt olika ut men ger exakt samma förutsägelser och resultat. Så småningom lyckades John von Neumann (ofta kallad Einsteins jämlike) visa att Schrödingers och Heisenbergs ansatser i själva verket är två olika tillämpningar av operatorer i ett abstrakt Hilbertrum (ett oändligtdimensionellt, euklidiskt rum). De två modellerna är således logiskt isomorfa, dvs har exakt samma logiska struktur. Det handlar helt enkelt om samma modell, uttryckt i två olika matematiska språk.
Ett annat exempel är gravitation, som både kan förklaras genom Newtons gravitationsteori (gravitationen är en avståndsberoende, attraktiv kraft som verkar mellan alla objekt som har massa) och Einsteins allmänna relativitetsteori (alla objekt som har massa "kröker" den omkringliggande rum-tiden). Att en kastad boll inte rör sig längs en rät linje utan följer en parabel (en krökt bana) beror, enligt Einstein, inte på att bollen påverkas av en kraft (jordens gravitationskraft), utan av att rummet och tiden är krökta på grund av jordklotets massa. Bollen går egentligen rakt fram (opåverkad av krafter), men eftersom rum-tiden är krökt blir "rakt fram" (kortaste avståndet mellan två punkter) en parabel i detta fall (eller om vi skall vara riktigt noggranna, den tredimensionella projektionen av den fyrdimensionella banan i rum-tiden blir en parabel). Både Newtons och Einsteins teorier (som ju förklarar gravitationen på helt olika sätt) kan fullt tillfredsställande förklara fenomenet gravitation (jag bortser här från extrema objekt som svarta hål och liknande, vilka Newtons teori inte kan handskas med). Till skillnad från de kvantmekaniska modellerna i föregående stycke så är relationen mellan de två gravitationsmodellerna oklar, och när nobelpristagaren Leon Ledermann efter sin nobelföreläsning på KTH 1988 fick frågan hur dessa två modeller relaterar till varandra, svarade han med ett spjuveraktigt leende, "You are not supposed to ask that question (Du förväntas inte ställa den frågan)".
Överfört på föreliggande diskussion om lyftkraft har vi sett i tidigare avsnitt av denna artikel att lyftkraften kan förklaras både genom att hänvisa till luft som accelereras nedåt (Newtons perspektiv) och genom att hänvisa till att det på en vinges ovansida finns ett undertryck som så att säga suger upp vingen (Bernoullis perspektiv). Här har vi således två modeller som kan förklara samma sak. Kanske är dessa två modeller helt enkelt logiskt ekvivalenta. Och kanske bygger båda modellerna på någon ännu mer grundläggande fysikalisk princip (som i fallet kvantmekanik). Eller kanske att de är relaterade till varandra på något annat sätt?
Till exempel skulle det kunna vara så att den ena modellen är en konsekvens av den andra, dvs den ena modellen kanske kan härledas ur den andra. Kanske är det helt enkelt så att en del av eller kanske hela undertrycket på en vinges ovansida orsakas av att vingen skyfflar stora mängder luft nedåt? Eller kan det vara tvärtom, dvs att vingen skyfflar luft nedåt på grund av undertrycket på vingens ovansida? Det senare verkar dock mindre troligt, eftersom jag inte kan komma på någon fysikalisk mekanism genom vilken detta skulle kunna ske.
Ovan har vi sett att det dynamiska trycket (ρv2/2) finns med både i Bernoullis lag (ekvation 1 i del 1), och i sambandet mellan lyftkraft och lyftkraftskoefficient etc (ekvation 2 i del 1), där det betecknas q. I den senare ekvationen ingår anfallsvinkeln som parameter (CL i formel 2 i del 1 är ju direkt proportionell mot anfallsvinkeln — se bild 5 i del 1). Bernoullis lag handlar om undertycket på en vinges ovansida, medan anfallsvinkel mer direkt handlar om att accelerera luft nedåt. Att samma faktor (dynamiska trycket) finns med i båda uttrycken tyder på att det under alla förhållanden finns en koppling mellan dessa två modeller för lyftkraft.
Ett propellerblad fungerar i princip exakt som en vinge (vilket redan bröderna Wright insåg). Bakom en roterande propeller blåser det rejält. Tror du mig inte, ställ dig alldeles bakom ett startande propellerplan! Framför propellern har vi i stället ett starkt sug (dvs vi har ett undertryck där). Går motorn på högvarv riskerar man att sugas in propellern om man kommer för nära. På jetmotorer är problemet ännu större och det har vid flera tillfällen hänt att människor sugits in i deras luftintag.
Under de år när Sverige hade runt 500 stycken J29 Flygande Tunnan (under 1950 och 60-talen), var det minst två flygmekaniker som sögs in i motorn och dog (J29 hade ett stort luftintag i nosen). Man skulle alltid ha ett skydd framför luftintaget när planet stod på marken, men ibland slarvade man tydligen. Det händer också idag att markpersonal sugs in i jetmotorer. Senast jag läste om detta var 2015, när en tekniker i Indien sögs in i en motor på en Boeing 747. Några år tidigare, på El Paso International Airport, sögs en tekniker in i en av motorerna på en Boeing 737, mitt under det att passagerarna höll på att gå ombord. En människa som står mindre är 7 m framför luftintaget på en Boeing-737-Max-motor med startpådrag (take off power) sugs obevekligt in i motorn. Även vid låga varvtal riskerar man att sugas in om man kommer för nära. Och även om man står vid sidan av luftintaget finns risken att man sugs in. Chansen att överleva är noll!
Frågar man sig vad som är orsaken till undertrycket framför en roterande propeller eller en jetmotor, så är det uppenbara svaret att propellern eller fläkten/kompressorn i jetmotorn skyfflar/accelererar luft bakåt. När luft strömmar till för att fylla ut undertrycket (som bildas när propellern eller kompressorn skyfflar luft bakåt), upplevs detta som ett sug (en gas går ju från högre till lägre tryck). Rimligen bör detta resonemang mer eller mindre också kunna tillämpas på en vinge.
Eftersom ett propellerblad fungerar som en vinge, kan man också säga att en vinge fungerar som ett propellerblad. Och precis som att propellerbladet, när det rör sig genom luften, ger upphov till ett undertryck framför propellern (dvs ett sug framför propellern) ger vingen, när den rör sig genom luften, upphov till ett undertryck ovanför vingen (propellern verkar ju horisontellt och skyfflar luft bakåt medan vingen verkar vertikalt och skyfflar luft nedåt, vid planflykt). Så man kan säga att Newton (tredje lagen om verkan och motverkan) och Bernoulli (summan av rörelseenergi och potentiell energi är konstant — se diskussionen om Bernoullis lag i inledningen till avsnittet "Bernoulli i nytt ljus") utgör två olika perspektiv på en och samma sak. Många mekaniska problem kan lösas antingen genom att man tittar på systemets energier eller att man tittar på de verkande krafterna. Krafter är direkt kopplade till rörelsemängd [rörelsemängden (p) hos ett objekt är lika med produkten av objektets massa (m) och dess hastighet (v), dvs p=mv — hastighet och rörelsemängd har både storlek och riktning, dvs är vektorstorheter, och anges därför med fetstil]. Kraft (F) är lika med tidsderivatan av rörelsemängden (F=dp/dt), dvs ett mått på rörelsemängdens förändring per sekund.
En vinge kan således betraktas som en linjär propeller som skyfflar (accelererar) luft nedåt (precis som att det finns linjära elmotorer, t ex de elektriska katapulterna på den senaste generationen av USA:s hangarfartyg), medan en propeller kan betraktas som en roterande vinge (eller snarare roterande vingar) som skyfflar luft bakåt.
Energi och rörelsemängd är fysikens två mest fundamentala storheter. Total energi och total rörelsemängd konserveras (bevaras) alltid i ett slutet system (ett system som inte påverkas av några yttre krafter och där ingen energi tillförs eller försvinner). Dessa konserveringslagar är två av fysikens mest grundläggande principer. I min artikel Fysik för fotgängare kan läsaren läsa mer om detta.
Ovanstående kan sammanfattas i:
Utifrån Bernoullis perspektiv (luftflödet på en vinges ovansida har högre fart än på undersidan vilket skapar ett lägre tryck på vingens ovansida) förklarar man en vinges lyftkraft genom att utnyttja energins konservering.
Utifrån Newtons perspektiv (vingen accelererar luft nedåt) förklarar man en vinges lyftkraft genom att utnyttja rörelsemängdens konservering.
Båda dessa ansatser leder fram till Bernoullis lag och i förlängningen samma aerodynamiska formler (t ex formel 2 i del 1), dvs ger samma praktiska resultat. Bernoullis lag kan dessutom bevisas både med hjälp av energiprincipen (energin konserveras i ett slutet system) och med hjälp av de grundläggande rörelselagarna i Newtons mekanik (och i förlängningen utifrån att rörelsemängden konserveras i ett slutet system). Den senare metoden har använts i min härledning av Bernoullis lag (som diskuteras ovan i avsnittet "Bernoulli i nytt ljus"). Av detta framgår hur fundamentalt dessa två ansatser är kopplade till varandra.
En ytterligare faktor som kan bidraga till lyftkraften är Coandaeffekten (se avsnittet "Bernoulli och Coandaeffekten" i del 1). Denna effekts bidrag till en vinges lyftkraft måste rimligen vara begränsat eller kanske minimalt (annat än i speciella fall — slats, blåsta klaffar och liknande).
Förutom att direkt skyffla luft nedåt genom sin anfallsvinkel (ungefär som en planka) gör en vinges form (vingprofilen) i kombination med dess anfallsvinkel att även luften som passerar ovansidan av vingen får en nedåtriktad komposant och därmed bidrar till lyftkraften (se bild 2 i del 1). Plus att vingens form och anfallsvinkel också har en ytterligare funktion; att ge luften på ovansidan högre fart (som således inte har något med Equal Transit Time att göra). Detta skapar, enligt Bernoullis lag, ett lägre tryck där, vilket ger ett ytterligare bidrag till lyftkraften.
De första flygande farkoster som människan konstruerade var ballonger och ända fram till början av 1900-talet menade många (även ingenjörer) att det i princip var omöjligt att konstruera flygande farkoster som var "tyngre än luft" (ända tills Bröderna Wright bevisade motsatsen 1904). Medan vi ändå diskuterar principer för flygning kan det därför, för fullständighetens skull, vara på sin plats att diskutera vad som ger en ballong dess lyftkraft. Förklaringen är den välkända Arkimedes Princip. Denna är mer känd i samband med båtar och säger att vattnets flytkraft är lika med vikten av den volym vatten som båten tränger undan när den placeras i vattnet (givetvis gäller Arkimedes Princip även för andra vätskor än vatten, men just nu talar vi om båtar och då är det vatten som gäller — som vi skall se i nästa stycke så gäller också samma princip för gaser). Lägger vi en sten på vattenytan så försvinner den under vattnet (dvs sjunker), helt enkelt eftersom den mängd vatten den tränger undan väger mindre än stenen själv (eftersom stenen har större densitet än vattnet). Lägger vi i stället en frigolitbit på vatten så flyter den väldigt högt på vattnet, eftersom den har mycket mindre densitet än vatten och därför bara behöver tränga undan en liten del av sin egen volym för att lyftkraften från vattnet skall balansera frigolitbitens vikt. Att fartyg av stål flyter beror på de utgörs av ett förhållandevis tunt skal av stål, plus spant av stål som ger stadga åt skrovet. Detta skal är sedan "fyllt" med luft till större delen. När ett fartyg sjösätts börjar det sjunka och tränger då undan mer och mer vatten ända tills vikten av det undanträngda vattnet är lika med fartygets vikt då fartyget slutar sjunka. Fartyget har då uppnått sitt jämviktsläge/flytläge. Ju kallare och saltare vattnet är desto högre flyter fartyget, eftersom vattnets densitet då är större. Och ju tyngre ett fartyg är lastat, desto lägre ligger det i vattnet (och har då större djupgående).
En ballong utnyttjar samma princip. Den flyter helt enkelt på luften. Vikten av den luft som ballongen tränger undan måste vara lika med vikten av ballongen med passagerare etc. Eller större om man vill stiga med ballongen. Eller mindre om man vill sjunka. Eftersom luft har väldigt låg densitet jämfört med vatten, måste en ballong tränga undan en väldigt stor volym luft för kunna bära t ex två personer plus ballongkorg plus vikten av ballongen själv med utrustning. För att det hela skall fungera måste själva ballongen vara fylld med en gas (som spänner ut ballongen), vilken måste ha betydligt mindre densitet än luft (idag ofta varmluft men även vätgas eller helium fungerar). Observera att ballongen även måste bära upp vikten av gasen inuti ballongen. Själva ballonghöljet måste vara tillverkat av ett synnerligen lätt material som har tillräcklig hållfasthet fast det är tunt. Att tillverka en ballong som "innehåller" vakuum (vilket vore det mest effektiva ur lyftkraftssynpunkt) kräver att ballonghöljet måste spänna ut sig självt genom någon struktur av aluminiumbalkar etc. Eftersom denna struktur måste hålla för den stora tryckskillnaden mellan normalt atmosfärtryck utanför ballongen och vakuumet inuti "ballongen" skulle vikten av "vakuumbehållaren" bli alldeles för stor.
Sammanfattningsvis: En ballong får lyftkraft genom att tränga undan luft med hjälp av en gas lättare än luft medan konventionella flygplan huvudsakligen skapar lyftkraft genom att skyffla luft nedåt, utnyttjande Newtons tredje lag. Likheten mellan båtar/fartyg och flygplan är större än man kanske tror innan man hunnit tänka djupare på saken. När det gäller fartyg skiljer man på deplacementsbåtar och planande båtar. En deplacementsbåt flyter enligt Arkimedes Princip (t ex roddbåtar, segelbåtar, handelsfartyg etc) och måste tränga undan väldigt mycket vatten för att ta sig fram, dvs kommer att ha stort vattenmotstånd och blir därmed ganska långsam alternativt bränsleslukande. En planande båt (de flesta snabbgående motorbåtar och vissa typer av militära fartyg) som uppnått planingsfart har bara en liten del av skrovet nere i vattnet och bärs huvudsaklingen upp av att skrovet har en sådan form att det accelererar vatten nedåt, varvid vattnet svarar med en motsvarande motkraft riktad uppåt, enligt Newtons tredje lag. Vid tillräckligt hög fart blir denna kraft tillräckligt stor för att bära upp båten. Stannar motorn eller man kör för sakta sjunker en planande båt ner och blir en deplacementsbåt (man kan säga att den stallar). Eller kanske sjunker (man kan köra snöskoter på vatten om man har tillräckligt hög fart, men underskrider man en viss fart sjunker scotern). Och analogt om motorerna på ett flygplan stannar. Då börjar planet sjunka och blir ett segelplan. Eller stallar om piloterna gör fel. Så man kan säga att ballonger är deplacementsflygfarkoster medan konventionella flygplan är planande flygfarkoster.

Dimbildning i luftintagen hos ett startande jetplan. Vid start använder man nästan full dragkraft på motorerna varför undertrycket framför luftintagen är större än normalt.
Vid vissa meteorologiska förhållanden kan man på startande jetplan se hur det bildas dimma i luftintagen till motorerna. Oftast är denna dimma inte konstant utan kommer och går (pulserar). Mekanismen bakom är samma som den dimbildning man ibland kan se på ovansidan av en vinge (se bild 17 i del 1) på grund av undertrycket där. Analogin mellan en propeller/jetmotor och en vinge framgår således på många olika sätt.
Dimbildning är kopplad till tre parametrar; luftens fuktighet, temperatur och tryck. När trycket sänks (vilket sker framför en jetmotors luftintag och på ovansidan av en vinge) så sänks också temperaturen, vilket innebär att lufttemperaturen närmar sig daggpunkten (där dimma utlöses). Förutsättningen för att dimma skall bildas är givetvis att luftfuktigheten är tillräckligt stor.

Ett ytterligare exempel på kopplingen mellan lyftkraft och att skyffla luft nedåt är Harrier Jump Jet. Ett brittiskt, vertikalstartande och -landande jakt-/attackplan (VTOL, vilket står för "vertical take off and landing"). Harriern har fyra vridbara huvudmunstycken, två främre som får kalluft från fläkten (se min artikel om jetmotorer, avsnittet om turbofläktmotorn) och två bakre som får varmluft från motorns utblås. Dessutom har man mindre, vertikala munstycken i vingspetsar och längst fram och längst bak för att kunna balansera planet, plus att man har små munstycken på flygkroppens sidor, vilka verkar horisontellt. Vid vertikalstart är de fyra huvudmunstyckena riktade nedåt och ger tillräckligt med lyftkraft för att planet skall stiga rakt upp. Efter starten vrider man försiktigt munstyckena så att de blir riktade mer och mer bakåt, varvid planet börjar röra sig framåt (de kan också riktas framåt, vilket leder till att planet backar). När farten ökar får vingarna alltmer lyftkraft och vid en viss fart bär vingarna planet och munstyckena är helt riktade bakåt och ger enbart dragkraft. Vertikalstart fungerar bara om planet är relativt lätt och normalt accelerar man planet på marken (med bakåtriktade huvudmunstycken) för att ge vingarna tillräcklig lyftkraft och sedan lättar man. Startsträckan blir i detta fall väldigt kort, kanske ett par hundra meter. Startsträckan kan förkortas ytterligare till 50-100 m om man startar via en ramp (som ser ut ungefär som en hoppbacke för skidor). I de senare fallen är munstyckena riktade snett bakåt/nedåt. Vid landning kan man oftast landa vertikalt, eftersom planet då är lätt (vapenlasten förbrukad och lite bränsle kvar). Detta kallas STOVL (short take off and vertical landing).
Harriern utgör ett utmärkt exempel på hur lyftkraft och dragkraft kan genereras med samma mekanismer (skyffla luft nedåt eller bakåt). Vid vertikalstart är det motorerna som skyfflar luft nedåt och vid normal flygning är det vingarna som skyfflar luft nedåt.
Så här långt verkar allting ganska klart. Men nu kommer vi in på lite mer osäker mark eller kanske snarare försåtminerad terräng. Aerodynamiker är överens om att den högre hastigheten på ovansidan av en vinge (oavsett dess profil) inte har något att göra med Equal Transit Time (ETT), dvs att luften som går över vingen och luften som går under vingen passerar vingen på exakt samma tid, utan den högre farten på ovansidan har en helt annan förklaring (vi återkommer alldeles strax till detta). Men oavsett förklaringen till den högre hastigheten så kommer denna högre hastighet att generera ett lägre tryck på vingens ovansida relativt undersidan (enligt Bernoullis sats), vilket skapar en lyftkraft, som bidrar till den totala lyftkraften.
Luftens högre fart på en vinges ovansida har två förklaringar (som båda bidrar till den högre farten):
Förklaring 1. Eftersom vingen skyfflar luft nedåt (vilket skapar lyftkraft i enlighet med Newtons tredje lag om verkan och motverkan) och därmed orsakar ett undertryck på vingens ovansida, kan vi tillämpa Bernoullis lag åt andra hållet. Denna lag säger ju att summan av det statiska och det dynamiska trycket är konstant. Om det dynamiska trycket ökar (dvs luftflödets fart ökar) kommer det statiska trycket att minska, dvs vi får ett undertryck (som i förklaring 2). Men motsatsen måste också gälla, dvs om det statiska trycket på en vinges ovansida minskar (t ex på grund av att den skyfflar luft nedåt), måste det dynamiska trycket där öka, dvs luftflödets fart på ovansidan måste öka. Generellt säger Bernoullis lag att när ett flöde (av gas eller vätska), vars energi är konstant, passerar ett område med lägre tryck så ökar dess fart och vice versa. Observera att det i detta fall är undertrycket som skapar den högre farten, dvs det motsatta mot förklaring 2 (där den högre farten skapar ett undertryck).
Förklaring 2. En del av luftens högre fart på vingens ovansida (utöver det bidrag till farten som diskuteras i förklaring 1) orsakas av vingens anfallsvinkel och form/profil (och inte av att ovansidan är mer krökt än undersidan och att luften på ovansidan har längre väg att gå). Denna högre hastighet, som således är aerodynamiskt genererad, kommer enligt Bernoullis lag att skapa ett lägre tryck på ovansidan av vingen, dvs bidrar till lyftkraften.
Både förklaring 1 och förklaring 2 bidrar således till luftens högre fart på vingovansidan. Och både förklaring 1 och förklaring 2 bidrar till undertrycket på vingens ovansida. Skillnaden, när det gäller undertryck, är att det undertryck som genereras av lyftskyfflandet nedåt (förklaring 1) inte bidrar till lyftkraften utan är genererat av lyftkraften (eftersom det orsakas av att luft skyfflas nedåt och därmed skapar lyftkraft). Endast den del av undertrycket som genereras enligt förklaring 2 bidrar till lyftkraften. Däremot bidrar förklaring 1 till luftens högre fart på vingens ovansida.
Observera, de två förklaringarna ovan (1 och 2) handlar primärt inte om hur en vinges lyftkraft genereras, utan de utgör två olika (och kompletterande) förklaringar till varför luftflödet på en vinges ovansida har högre fart än på undersidan. I det första fallet (förklaring 1) är luftens högre fart på vingens ovansida en konsekvens av att vi har ett lägre tryck där, vilket i sin tur är en konsekvens av att vingen skyfflar lyft nedåt, medan i andra fallet (förklaring 2) luftens högre fart på vingens ovansida (orsakad av vingens form och anfallsvinkel) genererar lyftkraft (men inte hela lyftkraften), Dvs enligt förklaring 1 bidrar inte luftflödets högre fart till lyftkraften.
Dvs för att sammanfatta: I förklaring 2 skapar således luftens högre fart på vingens ovansida en del av lyftkraften (genom det lägre tryck den högre farten genererar) medan i förklaring 1 lyftkraften (accelererande av luft nedåt) visserligen ger luften högre fart på vingens ovansida, men denna högre fart genererar inte någon lyftkraft utan är en konsekvens av att luft accelereras nedåt. Både förklaring 1 och förklaring 2 bidrar till luftflödets högre fart på vingens ovansida och både förklaring 1 och förklaring 2 bidrar till lyftkraften (förklaring 1 genom att skyffla luft nedåt och förklaring 2 genom att ge luften högre fart på vingens ovansida).
Låt oss nu repetera vad vi har kommit fram till hittills. Vi har således tre möjliga processer som bidrar till en vinges lyftkraft.
A. (förklaring 1 ovan). Att vingen skyfflar luft nedåt på grund av anfallsvinkel och profil.
B. (förklaring 2 ovan). Att luftens hastighet på vingens ovansida, på grund av vingens anfallsvinkel och profil, är högre än på undersidan, skapar ett lägre tryck på ovansidan.
C. Ett litet bidrag till lyftkraften ges av Coandaeffekten som beskrivs i del 1.
Enligt A, som jag gissar är huvudförklaringen till en vinges lyftkraft, skyfflar en vinge luft nedåt genom sin anfallsvinkel och profil. Detta ger en uppåtriktad kraft (lyftkraften), enligt Newtons tredje lag (om verkan och motverkan). Accelererandet av luft nedåt ger också ett undertryck på vingens ovansida. Detta undertryck skapar således inte lyftkraft utan genereras av att vingen skyfflar luft nedåt. Det senare orsakar lyftkraften medan undertrycket är en sekundäreffekt av detta (kausalt). I stället för att undertrycket genererar lyftkraft så genereras således undertrycket av lyftkraften (av accelererandet av luft nedåt).
Enligt B, som utgör en delförklaring till en vinges lyftkraft, gör en vinges form och dess anfallsvinkel att luften på vingens ovansida får högre fart än på undersidan. Denna högre fart skapar, enligt Bernoullis lag, ett lägre tryck på vingens ovansida än på dess undersida och denna tryckskillnad bidrar till lyftkraften.
Enligt C så bidrar också Coandaeffekten till lyftkraften. Förmodligen är detta bidrag litet i de flesta fall.
Bernoullis sats finns således med i bakgrunden i diskussionen om vingars lyftkraft. Denna lag förklarar varför luftflödet i förklaring 1/A ovan har högre hastighet på vingens ovansida. Den förklarar också varför i förklaring 2/B luftens högre fart på vingens ovansida (genererad av vingens form och anfallsvinkel) bidrar till lyftkraften.
Hur skall man då sammanfatta det vi kommit fram till? Ja, enligt min mening är det enklast och mest korrekt att se det på följande sätt (se också bild 1 nedan):
A. En vinge skyfflar luft nedåt på grund av sin anfallvinkel och form och fart (vilket ger större delen av en vinges lyftkraft). Detta skapar också, som en bieffekt, ett undertryck på ovansidan av vingen (som förklarats ovan), vilket gör att luftflödet där, enligt Bernoullis sats, får högre fart. Här skapas således den högre farten av undertrycket och undertrycket skapas av att luft skyfflas nedåt av vingen.
B. En vinges form, fart och anfallsvinkel ger högre fart hos luftflödet på vingens ovansida. Detta ger, enligt Bernoullis sats, ett undertryck där, vilket bidrar till lyftkraften. Här skapas således undertrycket av den högre farten och den högre farten skapas av vingens form och anfallsvinkel.
Summan av dessa två effekter (A och B) skapar den totala lyftkraften (vi bortser här från Coandaeffektens förmodat oansenliga bidrag). Hur stor del av lyftkraften som genereras av A respektive B beror antagligen på vingens form, anfallsvinkel och fart. Jag gissar (mellan tummen och pekfingret) att A genererar 80-90% av lyftkraften och B resten. När det gäller Coandaeffekten kanske det rör sig om någon bråkdel av en procent.
Både A och B ger en fartökning av luftflödet på en vinges ovansida (A på grund av det undertryck som genereras när en vinge accelererar luft nedåt, och B på grund av vingens form och anfallsvinkel). Den totala fartökningen på ovansidan av vingen är med andra ord lika med summan av A och B.
Summan av de två "undertryck" som på en vinges ovansida genereras av A och B ger det totala "undertrycket".
Slutsatsen av ovanstående blir att det finns två övergripande perspektiv man kan anlägga på genererandet av lyftkraften hos en vinge:
I. A och B ovan. Dessa två effekter är de effekter som orsakar lyftkraften. Punkt slut! Här betraktar man undertrycket på vingens ovansida, genererat av A, som en bieffekt (vilket det också är).
II. Man tittar på luftflödets totala fartökning på en vinges ovansida (vilken orsakas av både A och B) och använder sedan Bernoullis sats på flödets totala fartökning för att beräkna totala undertrycket på ovansidan av vingen (vilket i själva verket orsakas av både A och B) och därmed beräkna lyftkraften. Här kan man (formellt) betrakta accelererandet av luft nedåt som en bieffekt av undertrycket på vingens ovansida (fast det rent fysikaliskt, kausalt är tvärtom).
Observera: Punkterna I och II (ett och två i romerska siffror) ovan skall inte förväxlas med de tidigare punkterna (1, 2, A, B — C, dvs Coandaeffekten, lämnar vi därhän). I och II bygger på 1, 2, A och B och utgör två olika perspektiv på hur en vinges lyftkraft skapas; I (som innefattar A och B) och II (som tillämpar Bernoullis lag på luftens totala högre hastighet på ovansidan av vingen). Både I och II är giltiga (beräkningsmässigt) men den verkliga, kausala förklaringen till lyftkraften hos en vinge ges av I.
Notera att II inte handlar om hur totala lyftkraften verkligen skapas (den kausala orsaken till lyftkraften). En del av undertrycket på vingens ovansida bidrar inte kausalt till lyftkraften utan är (enligt A) en konsekvens av att vingen skyfflar luft nedåt (vilket skapar lyftkraft)! Utifrån mina erfarenheter från matematikens och fysikens värld är jag emellertid övertygad om att allting kommer att hänga ihop, även om man går "fel" väg (när det gäller kausalitet).
Utifrån den luft som accelereras nedåt kan man dels räkna ut hur mycket lyftkraft som detta genererar (enligt Newtons tredje lag) och dels hur stort undertryck som detta skapar på ovansidan av vingen. Dessa tre storheter hänger ihop matematiskt. Känner vi undertrycket på vingens ovansida kan vi således räkna ut lyftkraften (som rent kausalt inte skapas av detta undertryck utan av att vingen skyfflar luft nedåt).
Inom fysik och matematik spelar det ingen roll vilken väg man väljer för att beräkna något, så länge som man gör rätt (de val vi gör i vår analys av ett system kan ju inte påverka den fysikaliska verkligheten — så länge som valen är matematiskt och fysikaliskt korrekta). Dvs rent praktiskt kan man förklara lyftkraften hos en vinge genom att hänvisa till att luften har högre fart på ovansidan och sedan använda Bernoullis lag för att beräkna lyftkraften. Precis som man alltid gjort. Punkt slut! Business as usual!
Vid beräkningen av lyftkraften enligt II tittar vi på luftflödets fart på vingens ovan- och undersida. På ovansidan har vi betydligt högre fart än på undersidan och genom att använda Bernoullis lag kan vi beräkna lyftkraften. Även fast detta sätt att angripa problemet kommer att fungera så avspeglar det inte korrekt vad som är orsak och verkan, eftersom större delen av lyftkraften på vingens ovansida inte genereras av det undertryck som man kommer fram till genom Bernoullis sats. Större delen av detta undertryck skapas ju inte genom flödets högre fart på ovansidan av vingen utan av att vingen skyfflar luft nedåt och denna del av undertrycket bidrar inte till lyftkraften. Men beräkningsmässigt spelar det ingen roll, eftersom Bernoullis lag kan användas åt båda hållen. När den del av fartökningen hos luften, som orsakas av accelererande av luft nedåt, sätts in i Bernoullis lag, får vi som resultat det undertryck som svarar mot den lyftkraft som genereras av att vingen accelererar luft nedåt (Puh! Det nog bäst att läsaren tar en paus nu — varför inte ta en fika innan du fortsätter?!).
För att sammanfatta: Vet vi hur mycket luft som skyfflas nedåt av vingarna kan vi beräkna hur stort undertryck detta genererar på vingarnas ovansida. Och vet vi undertrycket på vingarnas ovansida kan vi beräkna hur mycket luft som vingarna skyfflar nedåt. Och vet vi luftens fart på ovan- och undersidan av vingarna kan vi beräkna undertrycket på ovansidan. Etc. Allt hänger ihop.
Innan läsaren gå vidare föreslår jag att läsaren klickar på denna länk för att komma till min korta artikel om det amerikanska spaningsplanet SR-71. Läs där vad jag skriver om motorernas luftintag på detta plan (i slutet av artikeln) och det undertryck som skapas framför dem. I princip handlar det om exakt samma sak som vad jag diskuterar ovan. Obs, denna artikel utgör ett viktigt komplement till föreliggande artikel, och kommer väsentligt att bidra till läsarens förståelse av lyftkraft!
Eftersom mina duktiga läsare inte bara är duktiga utan också är lydiga, har de nyss läst det jag skriver om SR-71. Därför passar det bra att nu undersöka varför inte det av luftskyfflandet nedåt orsakade undertrycket på vingens ovansida bidrar till lyftkraften. Problemet är att detta undertryck är en del av att skyffla luft nedåt och skulle detta bidra till lyftkraften skulle vi så att säga sälja vår lägenhet två gånger (samtidigt). Det är ju så bedragare opererar, men fysikens lagar fungerar inte så. I så fall skulle vi ju fördubbla, eller nästan fördubbla lyftkraften utan att vi betalar något för detta. Det vore underbara nyheter för flygplanstillverkare och flygbolag om så vore fallet. Och i så fall skulle ju en jetmotor (som principiellt arbetar på samma sätt, fast den skyfflar luft bakåt och inte nedåt) inte bara skapa dragkraft genom att accelerera gaser bakåt utan den skulle också skapa ungefär ytterligare lika mycket dragkraft genom det undertryck som finns framför luftintaget (vilket i likhet med att en vinge skyfflar luft nedåt uppstår som en konsekvens av att gaser i motorn accelereras bakåt). Dvs ytterligare underbara nyheter för flygplanstillverkare och flygbolag. När Lockheeds konstruktörer räknade formellt fann man således att undertrycket framför motorernas luftintag på SR-71 stod för 80% av dragkraften medan motorernas utblås endast stod för 20%. Så kan ju maffiarevisorer räkna men inte seriösa ingenjörer. Det här var givetvis ett internt skämt i Lockheedingenjörernas fikarum (även om siffran 80% var formellt korrekt). Undertrycket framför motorerna är helt och hållet konsekvensen av att motorerna suger in enorma mängder luft, som sedan accelereras bakåt. I själva verket genererar motorerna 100% av dragkraften, fast man genom att bolla med siffror kan räkna fram att undertrycket framför motorerna ger en drag(eller snarare sug-)kraft som är lika med 80% av motorernas nominella dragkraft. Observera att undertrycket står för 80% och accelererandet av luft bakåt står för 20%, vilket tillsammans blir hela motorns dragkraft lika med 100%. Det enda vi åstadkommit med denna meningslösa men roande kalkyl är att vi flyttat pengar från ett konto till ett annat (från utblåskontot till luftintagskontot), vilket inte påverkar den totala ekonomin (totala dragkraften) för ett företag (flygplan). Undertrycket framför motorerna har således inte ökat totala dragkraften utan vi har helt enkelt genom matematiskt formella beräkningar flyttat 80% av motorernas dragkraft till undertrycket framför motorerna. Detta kan vara intressant bokföringsmässigt men påverkar inte totala dragkraften, vilken är lika med motorernas dragkraft. Punkt slut! Givetvis kan undertrycket vara intressant rent aerodynamiskt och påverka utformningen av motorernas luftintag, men detta har inget med dragkraft att göra.
Tittar man på accelererandet av luft nedåt för sig och undertrycket på vingens ovansida för sig (och bortser från att det senare är konsekvensen av det första) hamnar man helt fel. Man måste titta på totala luftflödet både horisontellt och vertikalt när det gäller en vinge (eller horisontellt när det gäller en jetmotor) som en helhet, dvs titta på hela flödet, från luften ovanför och framför vingen som sugs mot vingen för att ersätta den luft som vingen skickat nedåt (när jag använder begreppen vertikalt/horisontellt avser jag ett flygplan som flyger horisontellt).
För att lättare förstå, låt oss titta på ett stillastående jetplan där motorerna arbetar för nästan fullt (t ex ett plan som står uppställt på startbanan och precis har dragit på take-off power men ännu inte släppt hjulbromsarna). Luften framför motorn accelererar nu in mot luftintaget, där vi rent formellt har ett undertryck (en gas går ju från högre till lägre tryck). Inuti motorn fortsätter luften att accelerera tills den "skjuts ut" ur motorn med maximal fart (en propeller fungerar på i princip samma sätt). Det är denna fartökning (accelereration) av luften som orsaker motorns dragkraft, enligt Newtons tredje lag. Luftens fartökning, från att den börjar sugas in mot luftintaget flera meter framför detta tills den lämnar motorns utblås, ger dragkraften. Även om planet rör sig framåt förändras ingenting mer än att vi får en konstant fartkomposant som adderas till luftens acceleration. Denna bidrar givetvis inte till dragkraften. Endast accelerationen av luft bidrar. Summa summarum är att man måste betrakta hela luftflödet, framför och inuti motorn. Betraktar man vad som sker inuti motorn för sig och det formella undertrycket framför luftintaget för sig (och tror att detta undertryck bidrar till dragkraften) hamnar man helt fel.
För en vinge är det lite mer komplicerat, eftersom luftens acceleration orsakas av flygplanets fart. För en motor är fartvinden parallell med den acceleration av luften som motorn genererar. När det gäller en vinge har vi en vinkel mellan fartvinden och den luft som accelereras nedåt. Men principen är densamma. Något som framgår av en hovrande helikopter. Som nämnts ovan så fungerar en propeller precis som en vinge. Helikoptern utgör en talande illustration av detta. Hos en helikopter skapas lyftkraften genom rotorn, som i princip är en stor propeller med vertikal axel, som roterar horisontellt och skyfflar luft nedåt (man kan också säga att rotorn är som roterande vingar, där varje rotorblad kan betraktas som en vinge). Och för en hovrande helikopter finns ingen fartvind som komplicerar det hela. Här har vi ett obrutet luftflöde där luft ovan rotorn accelereras ned mot rotorn och sedan genom denna, vilket skapar lyftkraften. När det gäller en vinge måste vi således, precis som när det gäller jetmotorer och propellrar, titta på hela luftflödet, i detta fall ovanför och framför vingen och sedan hur detta flöde genom vingens anfallsvinkel och form böjs av nedåt. Undertrycket på vingens ovansida är en del av detta flöde (accelerationen av luft nedåt börjar flera meter ovanför vingen eller helikopterrotorn) och utgör inte någon orsakande faktor när det gäller lyftkraft.
När jag började läsa fysik gick man på föreläsningar och hade en lärobok man läste i. Det första ämnet var grundläggande mekanik. Det är ju ett handfast och konkret ämne som ter sig ganska enkelt att förstå. Och jag upplevde att jag förstod i stort sett allt, både på föreläsningarna och i läroboken, och kände mig väldigt nöjd med mig själv. Men så skulle vi börja lösa problem och fick i uppdrag att lösa några hemuppgifter som vi nästa gång skulle gå igenom tillsammans. En av hemuppgifterna var lite svårare och jag vecklade in mig i alltmer komplicerade resonemang och till slut var jag inte längre säker på hur allt hängde ihop och vad som orsakade vad. Det gick bara runt runt i huvudet på mig. När vi sedan gick igenom denna uppgift tillsammans och jag fick se lösningen kände jag mig väldigt ödmjuk. Jag insåg att där hemma hade tankarna fladdrat ostrukturerat fram och tillbaka och jag hade vecklat in mig i cirkelresonemang. När man tränger in i matematikens och fysikens värld handlar det inte bara om att lära sig fakta. Man måste också lära sig att tänka rätt och att tänka metodiskt och strukturerat. Det tog mänskligheten tusentals år att lära sig tänka rätt och en individ har inte tusentals år på sig för att komma fram till hur man tänker rätt. Alltså måste man lära sig detta under utbildningen. Det är därför man har räkneövningar på alla kurser i matematik, fysik och liknande. Det är där man lär sig tänka rätt. Och det är där man inser att man inte har förstått så mycket som man trodde. Genom att lösa problem, gång på gång på gång, tränar man sig i att ta sina tankar tillfånga och strukturera dem. På tekniska utbildningar är det ofta mindre än hälften av eleverna som går på föreläsningar. De tycker de lika gärna kan sitta hemma och läsa i läroboken (om det inte är en osedvanligt duktig eller underhållande eller berömd föreläsare). Men på räkneövningarna deltar nästan alla studenter, eftersom de är livsviktiga. Utan dem överlever man inte.
Låt mig bara ta ett enkelt praktiskt exempel. När elever på högstadiet eller gymnasiet löser ekvationssystem (som innehåller flera obekanta och består av flera ekvationer) händer det att man, efter långa och mödosamma räkningar, kommer fram till x=x eller 3,5=3,5. Båda sambanden är helt korrekta, men triviala. Vi visste ju redan innan att x är lika med x. Sådana resultat får man när man gjort allt matematiska rätt (annars skulle man kanske fått att 3,5=17, vilket är fel). Felet man gjort är att man kanske omedvetet stoppat in en ekvation i sig själv. Dvs man har skrivit om ekvationen enligt algebrans regler så att den ser helt annorlunda ut och ser därför inte att man stoppar in ekvationen i sig själv. Resultatet blir då ett trivialt samband, typ 3,5=3,5. Det betyder att man inte tagit sina tankar till fånga, inte strukturerat dem, under lösningens gång. Det räcker således inte att man gör allt rätt enligt algebrans regler, man måste också tänka rätt och metodiskt övergripande. Att tro att undertrycket på en vinges ovansida bidrar till lyftkraften är helt i paritet med att stoppa in en ekvation i sig själv. Har man lite erfarenhet som fysiker inser man omedelbart att detta inte kan stämma.
Det finns dock ett litet aber som komplicerar hela resonemanget ovan. Eller i varje eventuellt komplicerar det hela (jag är inte säker här). Ovan har vi kommit fram till att vingens accelererande av luft nedåt skapar större delen av lyftkraften och dessutom skapar en del av undertrycket på vingens ovansida som en bieffekt av luftskyfflandet. Detta undertryck genererar i sig ingen lyftkraft utan är en konsekvens av skapandet av lyftkraft, men det kan användas för att förklara/beräkna en del av vingens lyftkraft (eftersom det är relaterat till accelererandet av luft nedåt). Frågan är dock om detta skapade undertryck svarar mot hela den lyftkraft som accelererandet av luft nedåt genererar. Det kan vara så, men jag är inte säker. I min artikel om det amerikanska spaningsplanet SR-71 (som läsaren förhoppningsvis läst alldeles nyss — om inte läs den nu!) framkommer det att när planet flyger mach 3 (3 gånger ljudets hastighet) så skapas ett undertryck framför luftintagen till motorerna. Detta undertryck "suger" så att säga planet framåt och formellt står det för 80% av dragkraften medan de gaser som blåses ut från motorn endast står för 20% av dragkraften. Observera att detta är formellt (precis som att det undertryck som skapas av en vinges accelererande av luft nedåt formellt kan användas för att förklara en del av lyftkraften hos en vinge). Stoppar man SR-71:s motorer så försvinner givetvis undertrycket framför luftintagen omedelbart. Vi har här en liknande situation som när det gäller vingars lyftkraft. Jetmotorer accelererar luft bakåt och som bieffekt får man ett undertryck framför luftintagen (som formellt står för större delen av dragkraften) medan vingar accelererar luft nedåt och som bieffekt får man ett undertryck på vingens ovansida. I fallet SR-71 står detta undertryck för 80% av drivkraften. Kanske är det på liknande sätt för en vinge, dvs att räknar man på det undertryck ovanpå en vinge som skapas av luftskyfflandet kanske detta bara förklarar en del av den lyftkraft som lyftskyfflandet ger (kanske 80%). Nu börjar det bli lite väl komplicerat så jag sammanfattar det jag skriver ovan i en figur och hoppas att det stämmer att en bild säger mer än tusen ord.

Observera! Eventuellt är FN=0 (se sista stycket före bilden), och vi kan då bortse från detta bidrag till lyftkraften. A och B hänvisar till dessa punkter i föregående avsnitt (En djupdykning).
Bild 1. I figuren utgår jag från att Newton (dvs accelererande av luft nedåt) står för 85% av en vinges lyftkraft medan Bernoulli (luften har högre fart på ovansidan av vingen, vilket skapar ett undertryck där) står för 15% (det vi kallar A och B i föregående avsnitt). Vidare antar jag att undertrycket som skapas av luftskyfflandet endast kan förklara 80% av den lyftkraft som luftskyfflandet genererar (här sneglar jag på SR-71). Resten av den lyftkraft som genereras av Newton kan endast förklaras av luftskyfflandet självt och bidrar inte till undertrycket på vingovansidan. De olika bidragen till totala lyftkraften (20% av 85%, dvs 0,20⋅0,85=0,17 etc) framgår av figuren (17% respektive 68%, vilket tillsammans blir 85%). Bernoulli står för 15% och 85%+15%=100%.
Siffrorna ovan är givetvis bara gissningar men det spelar ingen roll (fast jag skulle inte bli helt förvånad om de kanske ligger i närheten av verkligheten). Just nu diskuterar vi principen för hur lyftkraft genereras. Siffrorna varierar självklart mellan olika vingprofiler och varierar säkert också med anfallsvinkel och fart etc för en viss vingprofil). Skulle någon som arbetar med aerodynamik råka läsa denna text, tar jag gärna emot kommentarer och korrigeringar till det jag skriver här.
Förklaringar till figuren:
pN är det undertryck som genereras av att en vinge skyfflar luft nedåt. Detta utgör en del av undertrycket på vingens ovansida.
vN är den del av luftströmmens totala fart på vingens ovansida som (enligt Bernoullis lag) skapas av den luft som skyfflas nedåt. Dvs pN ger vN enligt Bernoullis lag. vN utgör en del av den luftflödets fart på vingens ovansida.
FN är den eventuella del av lyfkraften som inte "finns med" i undertrycket skapat av den luft som accelereras nedåt. FN spelar i sin egen division. Eventuellt är FN=0
vB är den del av luftströmmens totala fart på vingens ovansida som orsakas av vingens profil och anfallsvinkel. Farten vB (som inte har någon som helst koppling till accelererandet av luft nedåt) utgör således en del av luftflödets totala fart på vingens ovansida och skapar en del av vingens lyftkraft (gissningsvis ca 15%).
pB är det lägre tryck på vingens ovansida som orsakas av vB enligt Bernoullis lag (dvs enligt den gängse förklaringen av lyftkraft bortsett från den felaktiga teorin om Equal Transit Time). pB utgör en del av undertrycket på vingens ovansida och bidrar till ca 15% av lyftkraften.
I Newtons perspektiv orsakar en del av totala undertrycket (pN) på vingovansidan (skapat av lyftskyfflandet nedåt) en del av den högre flödeshastigheten (vN) på ovansidan. Medan i Bernoullis perspektiv en del av luftflödets högre fart (vB) på ovansidan (skapat av vingprofil och anfallsvinkel) genererar en del av totala undertrycket (pB) där.
Av figuren framgår att Newton (luftskyfflandet/Newtons tredje lag) skapar ett undertryck (pN), vilket i sin tur skapar en fartökning hos luftflödet på vingens ovansida (enligt diskussionen ovan). Detta undertryck (som är mätbart) kanske inte formellt förklarar hela lyftkraften genererad av luftskyfflandet, utan kanske bara 80%. Medan 20% av luftskyfflandelyftkraften kanske inte bidrar till undertrycket. Det sistnämnda bidraget till lyftkraften kallar jag FN. Till höger i figuren ser vi Bernoulli, där vingprofil och anfallsvinkel ger en ökning av luftflödets fart på vingovansidan (vB), vilket i sin tur leder till ett lägre tryck pB där (enligt Bernoullis lag) och därmed bidrar till lyftkraften.
Luftflödets totala fart på vingens ovansida ges av vtot = vN + vB och totala trycket där av ptot= pN + pB. Jag gissar att ptot och vtot hänger ihop via Bernoullis lag. Om FN=0 kan hela lyftkraften formellt (men inte kausalt) förklaras av ptot.
Observera att lyftkraften inte genereras av ptot (totala trycket på vingovansidan) om vi talar om fysikalisk orsak och verkan. Lyftkraften ges av tryckskillnaderna mellan trycken på ovansidan och undersidan av vingen, vilket vi kan kalla Δptot, där Δ står för skillnad/differens. Tryck definieras som kraft (F) dividerat med den area (A) som kraften verkar på, dvs p=F/A. Detta kan skrivas om som F=pA, dvs kraft är lika med tryck gånger area.
Detta leder fram till sambandet Flyft = Δptot⋅Avinge. Sambandet säger således att lyftkraften på en vinge är lika med tryckskillnaden mellan vingens ovansida och dess undersidan gånger vingarean. I verkligheten varierar trycket mellan olika delar av vingen varför man inte bara kan multiplisera tryck med area för att få kraften. I stället måste man uttrycka kraften genom en integral innehållande p och A (Flyft=∫ΔptotdAvinge). Eftersom vi just nu bara är intresserade av principer (det handlar ju inte om att räkna på verkliga vingar utan endast om att skapa en grundläggande förståelse för hur en vinges lyftkraft genereras) lämnar vi dessa tekniska detaljer därhän.
Figuren ovan står och faller således med huruvida hela det den lyftkraft som orsakas av en vinges accelererande av luft nedåt formellt kan förklaras av Δptot. Eller om det är som för SR-71, där hela dragkraften inte avspeglas i undertrycket framför luftintaget utan endast 80%. Om det första gäller, dvs om ptot=pN+pB utgör hela förklaringen till en vinges lyftkraft kan vi bortse från FN i figuren ovan och hålla fast vid den tidigare genomgången (I och II). Men om det är som hos SR-71 och en del av luftskyfflandet inte bidrar till undertrycket på vingovansidan så måste vi ha med FN i figuren. I så fall genereras totala lyftkraften av:
I praktiken kanske man inte behöver gå så djupt som jag gjort ovan, eftersom man kan baka in FN i de konstanter man sätter in i ekvationerna (om FN≠0). Ibland är saker och ting så komplicerade att man inte riktigt vet hur allting hänger ihop, men genom att anpassa sina formler till mätningar kan man få formlerna att ge korrekta förutsägelser trots att man bortser från eller gömmer undan vissa processer.
När is bildas på en vinges ovansida uppstår en potentiellt farlig situation, eftersom detta kan leda till att vingen stallar. Speciellt farligt är det om bara ena vingen stallar, eftersom man då riskerar att hamna i spinn. Relativt långsamma flygplan som inte flyger så högt (som turbopropplan) löper extra stor risk när det gäller isbildning (framför allt i samband med start och landning men även under cruise) och stor möda har lagts ned på att skapa olika typer av motmedel.
Vid nedisning är det framför allt de ytor som är riktade framåt som drabbas (på stabilisator, vingar och flygkropp). På vingarna ackumuleras ofta isen runt framkanten och sträcker sig en bit bakåt på både ovan och undersidan, dvs stör således strömningen på båda dessa sidor. Ofta drabbas tunna ytor, som stabilisator och vingspetsar, först, vilket leder till minskad kontroll i pitch- och rolled. Men isen inte bara stör luftflödet och därmed genererandet av lyftkraft utan skapar också ökad drag (vid svår isbildning kan luftmotståndet öka med upp till 500%!). Plus att planets vikt ökar (vid svår isbildning dramatiskt). Alla dessa faktorer degenererar flygplanets möjligheter att hålla sig i luften och försvårar manövreringen av planet. Isbildning är således inget att ta lätt på.
Men om nu, som jag påstår ovan, 85% av lyftkraften skapas genom att vingen skyfflar luft nedåt (enligt bild 1 ovan) tycker man att ett flygplan borde kunna hålla sig flygande även om främre delen av vingarna är kraftigt nedisad. Vingen borde ju fortfarandre fungera som en planka som skyfflar luft nedåt. Låt oss undersöka detta genom att gå till bild 1 ovan. Vi ser där att den del av lyftkraften som skapas genom att luft skyfflas nedåt, utan några andra effekter inblandade (FN — se texten efter bild 1 för förklaring) utgör ca 17% av den totala lyftkraften (siffrorna i denna bild får tas med en stor, stor nypa salt). Men 17% av den normala lyftkraften kan inte hålla planet flygande. Läsaren kanske då invänder att den del av lyftskyfflandet som, enligt diskussionen ovan, skapar ett delundertryck på vingens ovansida (pN), bidrar med ytterligare 68% av lyftkraften (se bild 1). Och det är sant. Men i detta fall är lyftskyfflandet inte renodlat à la planka (som de 17 procenten), eftersom det är kopplat till pN och därmed till luften ovanför vingen. Jag har i den tidigare texten liknat en vinge vid en propeller. Även propellrar löper risk att nedisas och turbopropplan har normalt elektrisk avisning av propellrarna. En nedisad propeller accelererar betydligt mindre luft bakåt, eftersom luftflödet genom propellern störs av ojämnheter på propellerbladen (det handlar ju inte bara om att skyffla luft bakåt utan det måste finnas tillgång till luft att skyffla bakåt).
Strömningslära är komplicerade saker och det visar sig att gas- och vätskeflöden har en tendens att "hålla ihop" och inte blanda sig med andra flöden (t ex så blandas den varma Golfströmmen endast obetydligt med det kallare vatten den strömmar genom på sin väg över Atlanten). Ovan har vi kommit fram till att en vinge som skyfflar luft nedåt får ett undertryck på ovansidan (och motsvarande för en propeller). Detta gör att ny luft strömmar till vingens ovansida så att mer luft kan skyfflas nedåt. Det handlar således om ett sammanhängande flöde från ovanför en vinge till under den. Störs luftflödet på vingens ovansida kan detta starkt påverka hur mycket luft som finns tillgänglig för att skyfflas nedåt. Till detta tillkommer att luften som passerar en vinges ovansida får en nedåtriktad hastighetskomposant (på grund av vingens form och anfallsvinkel), vilken bidrar till lyftskyfflandet nedåt (förutom den luft som skyfflas nedåt av vingens undersida — "plankeffekten") och om flödet på ovansidan störs så försvinner i värsta fall detta bidrag till lyftkraften. Plus att att den del av lyftkraften som genereras genom B (Bernoulli) i bild 1 också försvinner (15%). En vinges ovansida utgör således en viktig del i lyftkraftsskapandet och om ovansidan kontamineras av is så kommer vingen att tappa mycket av sin lyftkraft. Vilket leder till att man måste öka anfallsvinkeln, varvid luftmotståndet ökar ytterligare (utöver det ökade luftmotstånd som orsakas av isbildningen), vilket gör att farten går ned och man måste öka anfallsvinkeln ännu mer och vi har hamnat i en ond spiral. Och till slut är anfallsvinkeln så stor att luftmotståndet är större än motorernas dragkraft (även om vi har full dragkraft), varvid planet stallar.
För att sammanfatta sammanfattningen: Den högre farten på ovansidan av vingen beror således inte på Equal Transit Time (vingen mer krökt på ovansidan och luften har därför längre väg att gå där). I stället beror den högre farten på två faktorer; dels att när vingen accelererar luft nedåt på grund av sin anfallsvinkel och form, så uppstår ett undertryck på ovansidan, vilket enligt Bernoullis sats accelererar luftflödet där (dvs A), dels att vingen genom sin form och anfallsvinkel helt enkelt ger luftflödet högre fart på ovansidan (dvs B), vilket leder till lägre tryck hos luftflödet (enligt Bernoullis sats). Dvs totala undertrycket på en vinges ovansida består således, precis som totala farten, av två helt skilda komposanter. Men det spelar ingen roll. Vi kan räkna på fartökningen på ovansidan (utan att bry oss om att denna fartökning utgör summan av två olika mekanismer) och sedan med hjälp av Bernoullis sats räkna fram det undertryck som denna fartökning ger och sedan beräkna lyftkraften därifrån (under förutsättning att FN = 0). Dvs oavsett hur vi gör kommer vi att få samma resultat i våra beräkningar.
Dvs ytligt sett är allting precis som förut (under förutsättning att FN = 0), bortsett från att luftflödets högre fart på ovansidan inte orsakas av Equal-Transit-Time-modellen (fartökningen är dessutom större än vad ETT förutsäger). Vi kan helt enkelt nöja oss med att luftflödet har högre fart på ovansidan (utan att gå in på detaljer), vilket enligt Bernoullis lag ger ett undertryck där, som så att säga "suger upp" planet. Även om detta inte är den sanna förklaringen till lyftkraften (när det gäller orsak och verkan) så fungerar det som en formell förklaring. Och kan användas för beräkningar (eftersom Bernoullis lag fungerar åt båda hållen). Medan i själva verket lyftkraften orsakas av A och B ovan.
Vi har således två möjliga förklaringsmodeller; A/B (vilket vi kallar I i föregående avsnitt) respektive att undertrycket på vingens ovansida genererar hela lyftkraften (vilket vi kallar II i föregående avsnitt). Den första modellen är lika med den absoluta sanningen, den kausala förklaringen (så som det i själva verket är), medan den andra modellen vid beräkningar ger identiska resultat med den första modellen men inte stämmer med verkligheten (när det gäller vad som orsakar vad). Vilket påminner lite om de två gravitationsmodeller vi diskuterade i inledningen av föreliggande avsnitt. Einstein själv menade att man inte skulle dra för stora växlar på detta med den krökta rum-tiden och att det mer handlade om en användbar modell för gravitationen. Kanske att Newtons förklaring av tyngdkraften (gravitationen är en kraft) ligger närmare sanningen. På samma sätt kanske luftens högre fart på en vinges ovansida, vilken genererar ett undertryck där, kan ses som en användbar modell medan A/B ovan är den sanna förklaringen till en vinges lyftkraft. Jag gissar för övrigt att det är mycket enklare att räkna på (och framför allt mäta) undertryck på vingovansidan än att räkna på och mäta hur mycket luft som skyfflas (snett) nedåt och med vilken hastighet.
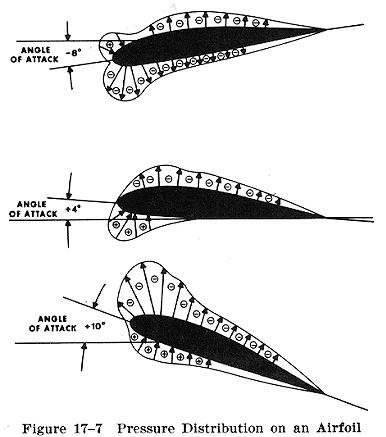
Bilden visar tryckfördelningen runt en vingprofil för tre olika anfallsvinklar (angle of attack). Vi ser här tydligt hur lyftkraften ökar med anfallsvinkeln. Observera att de uppåtriktade kraftvektorerna på vingens ovansida inte är resultatet av den felaktiga modellen ETT (Equal Transit Time), enligt vilken luften som strömmar längs den mer krökta ovansidan får högre fart på grund av den längre sträckan där (vilket enligt Bernoullis lag ger ett lägre tryck på ovansidan som suger upp vingen). Större delen av dessa uppåtriktade krafter är i stället resultatet av att vingen accelererar luft nedåt (enligt diskussionen ovan). Detta ger ett lägre tryck på vingens ovansida, vilket i sin tur, enligt Bernoullis lag, ger luftströmmen på ovansidan en högre fart. Dvs det är lyftkraften (skyfflandet av luft nedåt) och inte vingens större krökning på ovansidan, som genererar det mesta av den högre farten hos luftströmmen över vingen.
Jag förstår att det kan vara förvirrande för läsaren med de två bidragen till hastigheten hos luftflödet på en vinges ovansida; det ena hastighetsbidraget på grund av det undertryck som genereras av att vingen skyfflar luft nedåt och det andra på grund av att vingens form och anfallsvinkel ger luftflödet en högre fart på ovansidan. Läsaren kanske tycker att det verkar strida mot sunt förnuft att addera dessa två hastigheter, där den ena hastigheten orsakas av att lyftkraft skapas (genom att vingen skyfflar luft nedåt) medan den andra hastigheten skapar lyftkraft (eftersom den högre hastigheten ger upphov till ett lägre tryck på vingens ovansida). Så är dock inte fallet (motsvarande gäller för de två trycken). Inom fysiken finns en mycket viktig princip, superpositionsprincipen (fortsättningsvis kallad SP).
Låt mig ge ett par exempel på denna. När två ljusstrålar korsar varandra superponeras (överlagras) de två elektromagnetiska fälten och i det område där båda strålarna existerar (i den punkt där de korsar varandra) blir det elektromagnetiska fältet summan av de två fälten. Enligt SP växelverkar inte de två fälten med varandra i korsningspunkten och när de två strålarna skiljs åt så är strålarna identiska med innan de möttes.Låt mig ta ett annat exempel, tidvatten. 4/5 av tidvattnet på jorden orsakas av månen och 1/5 av solen. Soldygnet är 24 h (den tid det tar för jorden att vrida sig ett varv i förhållande till solen) medan måndygnet är 24 h 50 min (den tid det tar för jorden att vrida sig ett varv i förhållande till månen)
Att måndygnet är 50 minuter längre än soldygnet beror på att månen rör sig i sin ellipsformade bana runt jorden och när jorden vridit sig ett varv har månen hunnit förflytta sig och jorden måste rotera ytterligare i 50 minuter för att få månen i samma läge som dygnet innan).
Solen ger således upphov till en tidvattenvåg som rör sig runt jorden på 24 h medan månens tidvattenvåg behöver 24 h 50 min att gå runt jorden. Dessa två vågor samverkar med varandra och skapar det tidvatten vi får (på vissa ställen och vid vissa tidpunkter förstärker de varandra och på andra ställen och vid andra tidpunkter motverkar de varandra). Det finns också ett antal ytterligare tidvattenperioder som skapar sina tidvattenvågor (t ex får vi extra mycket tidvatten när månen är närmast jorden i sin bana och motsvarande när jorden är närmast solen). Etc. En gång vart 18:e år sammanfaller alla dessa deltidvatten och ger det högsta högvattnet (och det lägsta lågvattnet) under denna period som kallas Saroscykeln. Går man på grund vid högvatten denna dag måste man vänta i 18 år för att komma av grundet (alternativt att man ringer efter en bogserbåt och/eller ett mudderverk). När man gör tidvattentabeller lägger man ihop alla dessa deltidvatten, vilket man kan göra enligt superpositionsprincipen.
Man kan visa att superpositionsprincipen gäller för alla system som beskrivs av linjära differentialekvationer. Både elektromagnetisk vågrörelse och vattenvågor beskrivs av sådana ekvationer. Luftflödet runt en vinge likaså. Enligt SP kan man således lägga ihop de hastigheter och tryck vi behandlar ovan. Vilket underlättar våra beräkningar.
Ett undantag från SP när det gäller tidvatten, är att det kan vara så grunt i en havsvik så att vattnet inte räcker till för att ge summan av alla deltidvatten. Jag vill minnas att detta gäller området runt Southampton på Englands sydkust. Korsande laserstrålar av extrem intensitet beskrivs inte av linjära differentialekvationer så inte heller i detta fall gäller SP. Beträffande luftflödet runt en vinge så skulle det kunna vara så, när man närmar sig ljudets hastighet (kommer in i det transsoniska området), att kompressionseffekter uppstår, vilka gör att SP inte längre gäller. Eftersom vi i föreliggande framställning enbart diskuterar principen för hur lyftkraft skapas, håller vi oss utanför det transsoniska området.
Läsaren kanske tycker att jag är tjatig med alla sammanfattningar och repetitioner ovan. Men eftersom ämnet är komplicerat och det kan vara svårt att hålla alla bollarna i luften, så tror jag det är bra med upprepning. Repetition är ju all kunskaps moder sägs det. Vilket påminner mig om en doktorandkurs jag läste i kvantmekanik, där professorn inledde med att säga ungefär så här, "Ni har ju redan läst ett antal kurser i kvantmekanik och känner er antagligen förvirrade, vilket är helt naturligt. Alla blir förvirrade av kvantmekanik. Efter den här avancerade kursen kommer ni att känna er ännu mer förvirrade, men på en högre nivå."
När det gäller att populärvetenskapligt, pedagogiskt förklara hur en vinge skapar lyftkraft anser jag att man skall redovisa A och B ovan och bortse från den eventuella bidragande kraften FN (kanske att man på gymnasiets Naturvetenskapliga linje kan dra hela förklaringen). Att lyftkraft skapas genom att skyffla luft nedåt har de flesta människor inga svårigheter att förstå. Och att lämplig vingform och anfallsvinkel kan ge luften högre hastighet på ovansidan är inte heller svårt att förstå. Och så får man hänvisa till Bernoullis lag för att förklara varför den högre farten ger ett lägre tryck (den klassiska, felaktiga förklaringen hänvisar ju redan till Bernoullis lag). Här slipper man konstgreppet med ETT (som dessutom är felaktig).

Bild 2. Inverterad flygning. Vi ser här hur stor anfallsvinkeln är (planet nästan hänger i propellern. Ett normalt flygplan har vingarna monterade för att ha rätt anfallsvinkel (låt oss säga 5°) vid rättvänd planflykt med flygkroppen nära horisontell. Vid inverterad flygning måste man först ha en anfallsvinkel som kompenserar för den anfallsvinkel som vingarna monterats med (och som nu verkar åt fel håll) och sedan lägga till denna anfallsvinkel ytterligare en gång (dvs totalt 10°) för att få rätt anfallsvinkel. Men då har vi bortsett från att en vingprofil som är optimerad för att flyga rättvänt inte kommer att skyffla lika mycket luft nedåt, och inte kommer att öka luftflödets fart på vingens undersida (som nu är ovansida), lika mycket när man flyger inverterat. Alltså måste man ytterligare öka anfallsvinkeln för att kunna flyga horistontellt utan att sjunka (dvs flygkroppen kanske behöver ha en vinkel på 15°-20° relativt horisonten — givetvis beroende på farten, ju högre fart desto mindre anfallsvinkel måste ju gälla även vid inverterad flygning).
När en vetgirig elev frågar hur flygplan kan flyga upp och ned (inverterat), blir svaret ungefär följande, "På ett normalt flygplan, som inte är avsett för aerobatics (konstflygning), ges vingarna oftast en viss anfallsvinkel (för att skyffla luft nedåt) när de monteras på flygkroppen. Denna vinkel är lagom så att vingarna får rätt anfallsvinkel samtidigt som flygkroppen är nära horisontell. När man flyger upp och ned med ett sådant flygplan, måsta flygkroppen i sitt upp-och-nedvända läge ges en betydligt större anfallsvinkel för att skyffla tillräckligt med luft nedåt (se texten till bild 2 ovan). Plan avsedda för att flyga inverterat mer än under några sekunder (konstflygningsplan, jaktplan och liknande) har därför mindre eller ingen "inbyggd" anfallsvinkel hos vingarna plus att vingprofilerna är symmetriska eller nästan symmetriska. Ett problem med att flyga inverterat med "normala" kolvmotordrivna propellerplan är att de flesta sådana motorer (speciellt om motorn har förgasare) inte är gjorda för att operera upp och ned och därför kommer att stanna efter någon eller några minuter. Och motorn kan till och med skadas, eftersom den inte kommer att få tillräcklig smörjning. Kolvmotorer avsedda för aerobaticsplan etc måste därför anpassas så att smörjning och bränsleinmatning fungerar normalt även i inverterat läge.
Låt oss nu avslutningsvis, definitivt och slutgiltigt, krossa ETT-modellen (den vandringssägen som under mer än 100 år felaktigt påståtts vara förklaringen till vingars lyftkraft och som orsakat att många intresserade och smarta skolelever fått utskällning, kvarsittning och kanske smisk och sänkt betyg av sin fysiklärare för att de sagt emot vederbörande).
Det första felet med ETT (Equal Transit Time) är således att luftens högre hastighet på en vinges ovansida inte beror på olika krökningar av vingens ovan- och undersida (även hos vingar med samma krökning på båda sidorna har luften högre fart på ovansidan). Förklaringen ligger i stället i det undertryck som skapas på en vinges ovansida när den skyfflar luft nedåt (förklaring 1 ovan) och hos vingens aerodynamik (förklaring 2 ovan). Betrakta följande bild:

Bild 3. Bilden visar luftflödet runt en klassisk vingprofil. Pilarna visar luftströmningens riktning och hur tätt strömningslinjerna ligger är ett mått på luftens hastighet relativt vingen (ju tätare de ligger desto större är luftens hastighet). Vinkeln mellan de svarta räta linjerna är vingens anfallsvinkel. Vi ser att hastigheten hos luften är högre på ovansidan än på undersidan.
Enligt förklaring 1 ovan orsakas luftens högre hastighet på vingens ovansida av att vi har ett undertryck där (på grund av att vingen skyfflar luft nedåt) och att detta undertryck, enligt Bernoullis lag, ger luften högre hastighet (sjunker trycket ökar farten).
Enligt förklaring 2 ovan orsakas luftens högre hastighet på vingens ovansida av att strömningshastigheten generellt ökar vid utskjutande och konvexa ytor (exempelvis frampartiet av ett flygplan eller en vinge och minskar vid inbuktande ytor (framför allt bakpartiet av flygplanet). Kantiga ytor kan ge liknande effekter (detta diskuteras närmare i min artikel "Luftmotstånd (drag) och lyftkraft (lift)" i punkt 4 i avsnittet "Vågluftmotstånd"). Det är ungefär samma sak som när man håller fingret framför en del av öppningen hos en vattenslang varvid vattnet sprutar mycket längre (eftersom det får högre fart). Genom en kombination av anfallsvinkel och lämplig form på vingens framkant kommer luften på vingens ovansida att ha högre hastighet än på undersidan.
I praktiken bidrar både förklaring 1 och 2 till flödets högre hastighet på en vinges ovansida. Proportionerna mellan dessa bidrag varierar antagligen mellan vingprofil, anfallsvinkel och fart.
Ingen av dessa 2 förklaringar har något att göra med Equal Transit Time eller att vingen är mer buktad på ovansidan.
Fel nummer två med ETT-modellen är att luftmolekylerna Vera och Kurt inte har stämt möte vid vingens bakkant. Holger Babinsky, professor i aerodynamik vid universitetet i Cambridge, visar detta i ett mycket illustrerande vindtunnelförsök. Han har placerat en symmetrisk vingprofil med en viss anfallsvinkel (ca 10°) i en vindtunnel och gör luftströmningen synlig genom att spruta in rök"strålar" i vindtunneln. Genom att pulsa röken, dvs inte spruta in den kontinuerligt utan i korta pulser, kan man tydligt se strömningen runt vingen.



Bild 6. Vi ser redan här att luftströmningen på vingens ovansida har betydligt högre fart än den på undersidan.

Bildserien ovan gör en gång för alla slut på Equal-Transit-Time-modellen. Det finns dessutom ingen fysikalisk princip eller mekanism som kan förklara varför luftflödena på en vinges ovan- respektive undersida skulle vara synkroniserade på det sätt som ETT anger!
Klicka här för att se en video (ca 15 min), där man bl a får se den videosekvens i slowmotion som bilderna 4-7 ovan är hämtade från. Videon finns på youtubekanalen "Fly with Magnar". Kanalen drivs av Magnar Nordal, som är flygkapten och flyginstruktör. Här finns många intressanta videor. Det viktigaste i den video jag länkar till är sekvensen från professor Babinskys vindtunnelförsök och insikten att lyftkraftgenerering både kan förklaras med hjälp av energins bevarande och rörelsemängdens bevarande i ett slutet system.
Klicka här för att läsa en kort artikel om roterande cylindriska vingar, vilken förhoppningsvis fördjupar läsarens förståelse av lyftkraft.
Lyftkraft kan således förklaras både utifrån Bernoullis perspektiv (undertryck på vingens ovansida, vilket förklaras med hjälp av energins konservering) och utifrån Newtons perspektiv (skyffla luft nedåt, vilket förklaras med hjälp av rörelsemängdens konservering). Bernoullis ekvation (ekvation 1 i del 1), som är grundläggande inom aerodynamiken, kan härledas utifrån båda dessa perspektiv. Bernoullis perspektiv kan i sin tur, åtminstone delvis, förklaras av Newtons, dvs skyffla luft nedåt skapar ett undertryck på vingens ovansida. Att en vinge verkligen skyfflar luft nedåt framgår klart av bild 10 och 11 i del 1 (se länk i slutet av denna artikel). Samtidigt kan man (eventuellt, om FN = 0), som visats i föregående avsnitt, förklara hela lyftkraften med Bernoullis lag utifrån detta undertryck. vilket sammanlagt orsakas av två helt olika mekanismer (A och B ovan). I den senare förklaringsmodellen bortser man från luftskyfflandet.
Genom sin anfallsvinkel och genom sin form skyfflar således en vinge luft snett nedåt. Detta genererar förutom lyftkraft också inducerat drag (luftmotstånd), eftersom motkraften från luften (som verkar på vingen) kommer att vara riktad snett bakåt. En vinge kommer därför att förutom av lyftkraften (som är vertikal vid horisontell flygning) också påverkas av en bakåtriktad kraftkomposant, vilken verkar som ett luftmotstånd. Detta kallas inducerat luftmotstånd (induced drag) och växer när anfallsvinkeln och därmed lyftkraften ökar. När man tar fram nya vingprofiler försöker man optimera formen så att det inducerade luftmotståndet blir så litet som möjligt i förhållande till lyftkraften. Problemet med en helt plan (plankformad) vinge är att luftmotståndet växer så snabbt med anfallsvinkeln (genom att det i detta fall uppstår en enorm turbulens på ovansidan) att en sådan vinge är helt oanvändbar i praktiken (induced drag diskuteras närmare i min artikel om luftmotstånd och lyftkraft — scrolla ned till avdelningen "Inducerat luftmotstånd"). Alltså är en vinges form oerhört viktig för dess funktion.

Bild 8. USA konstruerade i slutet av 1950-talet ett sexmotorigt bombplan, XB-70 Valkyrie (planet var tänkt att heta B-70 och "X" står för experimentplan), med en planerad operativ hastighet av mach 3 (tre gånger ljudets hastighet). Uppgiften skulle vara att bära kärnvapen in i Sovjet i händelse av en storkonflikt mellan USA och Sovjet. Detta var mitt under kalla kriget och när Sovjetledningen fick kännedom om Valkyrieprojektet blev man synnerligen nervös. Det skulle rimligtvis dröja många år innan Sovjet kunde få fram ett motmedel mot Valkyrie. Två XB-70 byggdes och gjorde ett antal provflygningar och under några av dessa uppnådde man mach 3.04 och topphöjden 74 000 ft. Kostnaderna skenade dock iväg (som vanligt) och kritikerna argumenterade att interkontinentala kärnvapenrobotar kunde utföra samma uppgift som XB-70, men till en betydligt lägre kostnad. Det hela slutade med att projektet skrotades.
Under utvecklingen av XB-70 upptäckte man en ytterligare möjlighet att ge ett flygplan lyftkraft, nämligen att låta planet "rida på" den kompressionsvåg som uppstår vid supersonisk fart (överljudshastighet). Detta kallas compression lift. När en vinge genererar lyftkraft enligt genomgången ovan, skapas dessvärre samtidigt drag, dvs luftmotstånd (läs mer om detta här). Ju mer lyftkraft desto mer drag. Kompressionsvågsgenererad lyftkraft ger inte någon ökning av drag (bortsett från att så hög fart rent allmänt ger ett stort luftmotstånd), vilket ger en fördel i form av ökad räckvidd alternativt högre fart. För att hålla kompressionsvågen på plats under planet fälldes yttre delen av vingarna ner under flygning (se bilden ovan).
Så här ser vi ytterligare ett sätt att skapa lyftkraft hos ett flygplan. I detta fall fungerar det dock bara på dedicerade överljudsplan, som huvudsakligen flyger supersoniskt, dvs snabbare än ljudet. Normala stridsplan, som JAS Gripen, vilka har kapacitet att flyga mach 2, kan bara göra detta under några procent av flygtiden. Jag har inga siffror för JAS men en jämförbar F-16C kan flyga runt 9 minuter supersoniskt (utan yttre, fällbara extratankar, vilka drar ner farten och ökar bränsleförbrukningen) med maximalt motorpådrag, dvs med full efterbrännkammare. Dessutom misstänker jag att man måste flyga med hög supersonisk fart, nära mach 3, för att kompressionsvågsbaserad lyftkraft skall vara en betydande faktor.
Ovanstående utgör, trots att det blev ganska långt, endast en ytlig betraktelse över detta med lyftkraft. Vi ser här hur komplicerat allt blir när man försöker tränga in i ett område för att verkligen förstå. Inom teknik och naturvetenskap finns sällan enkla svar på våra frågor. Verkligheten är komplex och människan har att acceptera detta. Och detta är ju populärvetenskapens dilemma. Dvs att antingen göra stoffet så lättillgängligt så att det i praktiken blir mer fel än rätt (som den gängse, populära förklaringen av en vinges lyftkraft), eller med andra ord att man lurar läsaren, så att läsaren tror sig förstå, men det läsaren förstår är en så grov vrångbild av hur det verkligen förhåller sig, att det hade varit bättre att inte veta något alls. Eller också gör man ett ärligt försök att förklara, men då blir det ofta så komplext att få läsare orkar läsa texten. Stephen Hawking (1942-2018), den gravt handikappade, rullstolsbundne fysikern som ofta framträdde i olika tv-program, skrev för många år sedan (1988) en bok, A Brief History of Time. Boken såldes i över 10 miljoner exemplar och översattes till 35 språk och låg i många länder på bestsellerlistan i flera år. I boken försöker Hawking reda ut den moderna fysikens bild av vårt universum. Och han gör verkligen ett ärligt försök att ge en sann och korrekt bild. Jag minns att den fanns i travar i alla bokaffärer (på den tiden var Internetbokhandel ett okänt begrepp). Jag vill också minnas att den utnämndes till årets julklapp när den kom. Någon kallade lite elakt Hawkings bok för "Världens mest olästa bok". Dvs den finns i mer än tio miljoner bokhyllor runt om i världen men är läst i sin helhet av ett fåtal. Hawkings bok utgör tyvärr ytterligare ett exempel på populärvetenskapens och populärteknikens dilemma. Antingen blir det så ytligt och förenklat att det blir mer fel än rätt, dvs det hade varit bättre att läsaren aldrig läst boken i fråga, eftersom denne då vetat att han inte visste något i ämnet. Eller också blir det så komplicerat (precis som verkligheten ofta är) att ingen orkar läsa boken eller så svårt att den som orkar läsa boken ändå inte förstår något (mer än att ämnet är svårt — och det kan ju vara en värdefull insikt i sig).
Addendum (250325): Jag hittade idag ett intressant fotografi. Det är taget i en vindtunnel och visar strömningslinjer runt en helt symmetrisk vingprofil.

Bild 9. Ju tätare strömingslinjerna ligger desto större är, som konstaterats ovan, luftens fart. Vi ser tydligt att luften har betydligt högre fart på ovansidan. Förklaringen till luftens högre fart på den symmetriska vingprofilens ovansida är således inte Equal-Transit-Time (eftersom vingprofilen är symmetrisk) utan luftflödet skapas av vingprofilens form och dess anfallsvinkel.
Bilden visar exakt samma sak som bilderna 4-7, fast på ett något annorlunda sätt. Jag hoppas att jag med bilderna och argumenteringen ovan lyckats övertyga eventuellt tvivlande läsare att Equal-Transit-Time-modellen är falsk.